# 2024vldb: Efficient Exact Subgraph Matching via GNN-based Path Dominance Embedding

Efficient Exact Subgraph Matching via GNN-based Path Dominance Embedding

实现基于图神经网络（GNN）的路径嵌入框架（GNN - PE）的精确子图匹配

研究背景和目标
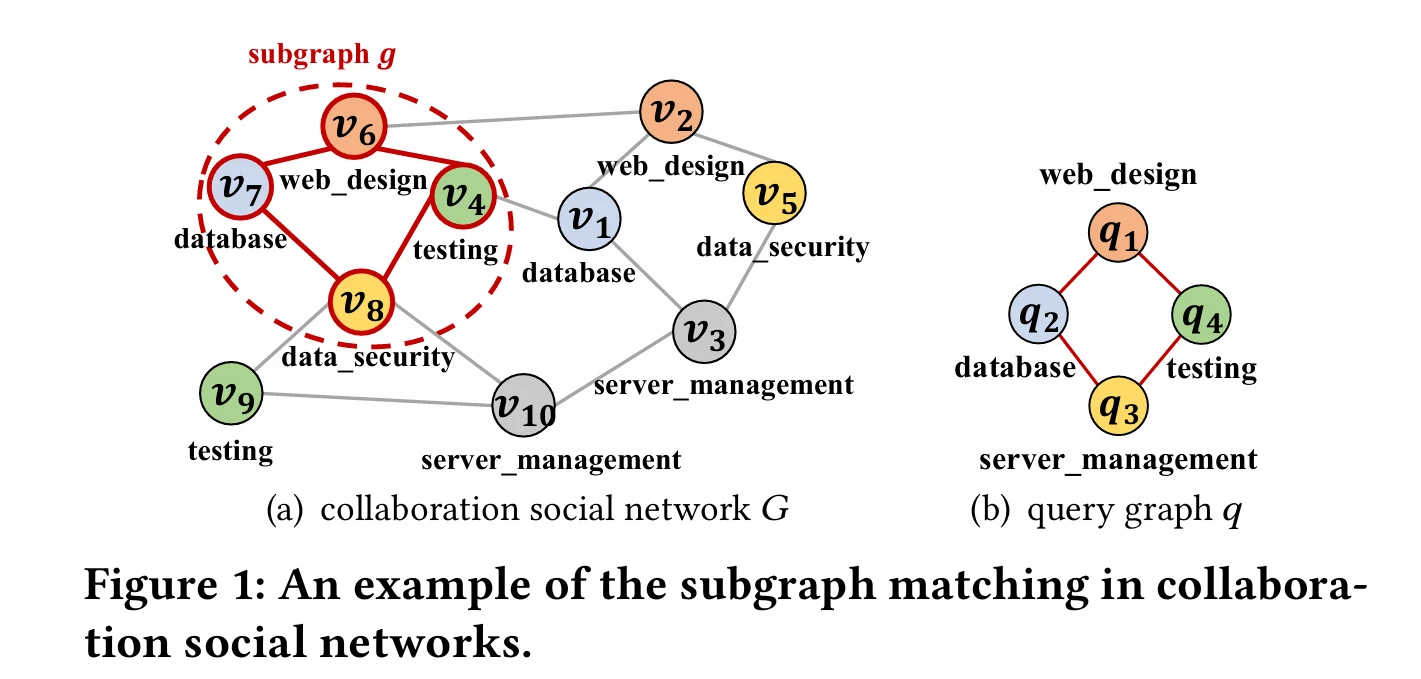
- 问题定义：精确子图匹配问题是在大规模数据图中找到与给定查询图同构的子图，在语义网、社交网络分析、知识图谱等诸多领域有重要应用。
- 传统方法的不足：传统基于 GNN 的图嵌入方法只能产生近似子图匹配结果，本文旨在提出一种能实现高效精确子图匹配的方法。
GNN - PE 框架原理
- 路径嵌入：精心设计基于 GNN 的路径嵌入，使得两条具有子图关系的路径（包括顶点的 1 - hop 邻居）的嵌入向量严格遵循支配关系。
- 索引构建：在路径嵌入向量上构建多维索引，通过遍历图分区上的索引来进行精确子图匹配。
- 剪枝策略：基于路径标签 / 支配嵌入提出有效的剪枝策略，保证子图匹配没有错误排除（false dismissals）。

[!note]
子图匹配的重要性：精确子图匹配在社交网络分析、知识图谱、生物网络等诸多领域有重要应用，但该问题是 NP - 完全问题，计算成本高。
传统方法的不足
一些工作通过牺牲准确性获取近似子图匹配结果，如使用图相似性度量搜索 k 个最相似子图，或利用 GNN 进行近似匹配，但缺乏准确性保证且不适合检索匹配子图位置。
传统基于 GNN 的嵌入方法只能产生近似结果，无法满足精确匹配需求。

Moreover, several recent works [6, 39] utilized deep-learningbased approaches such as Graph Neural Networks (GNNs) to conduct approximate subgraph matching. Specifically, GNNs can be used to transform entire (small) complex data graphs into vectors in an embedding space offline. Then, we can determine the subgraph relationship between data and query graphs by comparing their embedding vectors, via either neural networks [6] or similarity measures (e.g., Euclidean or Hamming distance [39]). Although GNN-based approaches can efficiently, but approximately, assert the subgraph relationship between any two graphs, **there is no theoretical guarantee about the accuracy of such an assertion, which results in approximate (but not exact) subgraph answers. ** Worse still, these GNN-based approaches usually work for comparing two graphs only, which are not suitable for tasks like retrieving the locations of matching subgraphs in a large-scale data graph.

Our Contributions. In this paper, we focus on exact subgraph matching queries over a large-scale data graph, and present a novel GNN-based path embedding (GNN-PE) framework for exact and efficient subgraph matching. In contrast to traditional GNN-based embeddings without any evidence of accuracy guarantees, we design an effective GNN-based path dominance embedding technique, which trains our newly devised GNN models to obtain embeddings of nodes (and their neighborhood structures) on paths such that: any two paths (including 1-hop neighbors of vertices on them) with the subgraph relationship will strictly yield embeddings with the dominance [14] relationship. This way, we can transform our subgraph matching problem to a dominating region search problem in the embedding space and guarantee a 100% recall ratio so that we do not miss any query results. In other words, we can retrieve candidate paths (including their locations in the data graph) matching with those in the query graph with no false dismissals. Further, we propose an effective approach to enhance the pruning power by using multiple sets of GNN-based path embeddings over randomized vertex labels in the data graph.

具有子图关系的任意两条路径（包括顶点的 1 - hop 邻居）将严格产生具有支配 [14] 关系的嵌入。通过这种方式，我们可以将子图匹配问题转化为嵌入空间中的支配区域搜索问题，并保证 100% 的召回率
换句话说，我们可以检索与查询图中路径匹配的候选路径（包括它们在数据图中的位置），且不会有错误排除。此外，我们提出了一种有效的方法，通过在数据图中对随机化的顶点标签使用 多组基于 GNN 的路径嵌入 来增强剪枝能力。

# 问题定义

图数据模型
- 定义了无向、有标记图 $G$ 的模型为四元组 $(V(G),E(G),\phi(G),L(G))$ ，其中 $V(G)$ 是顶点集， $E(G)$ 是边集， $\phi(G)$ 是顶点到边的映射函数， $L(G)$ 是给顶点标记的函数。
图同构
- 给出了无向、有标记图之间经典图同构问题的定义。两个图 $G_{A}$ 和 $G_{B}$ 同构（ $G_{A}\equiv G_{B}$ ）是指存在一个保持边的双射函数 $f$ ，满足顶点标记相同且边的对应关系也成立。同时还定义了子图同构（ $G_{A}\subseteq G_{B}$ ），即 $G_{A}$ 与 $G_{B}$ 的一个诱导子图同构，且子图同构问题是 NP - 完全问题。
子图匹配查询
- 定义了在大规模数据图 $G$ 上的子图匹配查询，即检索出与查询图 $q$ 同构的所有子图 $g$ （ $g\equiv q$ ），并强调本文考虑的是精确子图匹配，不同于近似子图匹配。
基于 GNN 的子图匹配框架
- 介绍了一种基于 GNN 的路径嵌入（GNN - PE）框架，用于高效回答子图匹配查询，包括离线预计算和在线子图匹配两个阶段。离线预计算阶段是对数据图 $G$ 进行预处理，构建路径嵌入向量的索引；在线子图匹配阶段是基于索引回答查询。
GNN - PE 框架的贡献
- 提出了基于 GNN - PE 框架用于精确子图匹配，设计了有效的基于 GNN 的路径支配嵌入方法用于精确子图检索，开发了高效的并行子图匹配算法，设计了新的成本模型用于选择最佳查询计划，并通过实验验证了该方法在真实 / 合成图上精确子图匹配的效率和有效性。

That is, we first pre-process the data graph 𝐺 offline by building indexes over path embedding vectors via GNNs (lines 1-5), and then answer online subgraph matching queries over indexes (lines 6-11).

For the detailed descriptions, please refer to our technical report [64].

# GNN-BASED DOMINANCEEMBEDDING

# GNN Model for the Node Embedding

GNNmodel

The GNN model consists of GAT [58], readout, and fully connected layers.

[!tip]
图注意网络（Graph Attention Network，GAT）是一种 基于空间域的图神经网络，其与传统的图卷积网络（GCN）等方法不同之处在于 引入了注意力机制。

节点嵌入的 GNN 模型结果
- 输入层：输入层。如前文所述，GNN 模型的输入是一个单位星图 $g_{v_i}$ （或者其星子结构 / 子图，记为 $s_{v_{i}}$ ）。 $g_{v_i}$ （或者 $s_{v_{i}}$ ）中的每个顶点 $v_{j}$ 都关联一个大小为 $F$ 的初始特征向量 $x_{j}$ ，而该向量是通过 顶点标签编码或者独热编码 [12] 获得的。
- 隐藏层：
  - GAT 层：计算顶点间的注意力系数 $ac_{v_{i}v_{j}} = a(Wx_{i},Wx_{j})$ ，
    然后归一化得到 $\alpha_{v_{i}v_{j}}=softmax(ac_{v_{i}v_{j}})$ ，
    GAT 层输出 $x_{i}'=\sigma(\sum_{v_{j}\in N_{v_{i}}}\alpha_{v_{i}v_{j}}Wx_{j})$ ，
    采用多头注意力机制时 $x_{i}'=\parallel_{k = 1}^{K}\sigma(\sum_{v_{j}\in N_{v_{i}}}\alpha_{v_{i}v_{j}}^{(k)}w^{(k)}x_{j})$ 。
  - Readout 层：对单位星图 $g_{01}$ 生成嵌入向量 $y_{i}=\sum_{\forall v_{j}\in V(g_{v_{i}})}x_{j}'$ 。
  - Fully Connected Layer：得到中心顶点 $v_{i}$ 的嵌入向量 $o(g_{v_{i}})=\sigma(\mathbb{W}y_{i})$ ，这里 $\sigma(\cdot)$ 是激活函数（如 Sigmoid 函数 $\sigma(x)=\frac{1}{1 + e^{-x}}$ ）， $\mathbb{W}$ 是全连接的权重矩阵。
    MLP 是多层全连接
- 输出层：输出 $o(g_{D_{i}})$ 作为中心顶点 $v_{i}$ 的嵌入向量 $o(v_{i})$ 。
  最终的全连接结果
  也可以看成是编码 + 深度学习
节点支配嵌入结果及表达式
- 损失函数：设计的损失函数 $L(D_{j})=\sum_{\forall(g_{v_{i}},s_{v_{i}})\in D_{j}}\parallel max\{0,o(s_{v_{i}})-o(g_{v_{i}})\parallel_{2}^{2}$ ，其中 $D_{j}$ 是包含单位星图 $g_{v_{i}}$ 及其子结构 $s_{v_{i}}$ 的训练数据集， $o(g_{v_{i}})$ 和 $o(s_{v_{i}})$ 分别是它们的嵌入向量。
- 节点支配关系：当损失函数 $L(D_{j}) = 0$ 时， $o(s_{v_{i}})$ 支配 $o(g_{v_{i}})$ （即 $o(s_{v_{i}})\leq o(g_{v_{i}})$ ），意味着对于子图关系的 $s_{v_{i}}$ 和 $g_{D_{i}}$ ，其嵌入向
  量满足支配关系。
路径支配嵌入结果及表达式
- 对于路径 $P_{z}$ ，其路径嵌入向量 $o(p_{z})=\parallel_{\forall v_{j}\in p_{z}}o(v_{j})$ ，如果路径 $p_{q}$ （及顶点的 1 - hop 邻居）是 $p_{z}$ （及顶点的 1 - hop 邻居）的子图，则 $o(p_{q})\leq o(p_{z})$ 。

To stabilize the learning process of self-attention, GAT uses a multi-head attention mechanism similar to [57], where each head is an independent attention function and 𝐾 heads execute the transformation of Eq. (3) in parallel. Thus, an alternative GAT output $x_{i}'$ can be a concatenation of feature vectors generated by K heads:

$x_{i}'=\parallel _{k = 1}^{K} \sigma\left(\sum_{v_{j} \in N_{v_{i}}} \alpha_{v_{i} v_{j}}^{(k)} w^{(k)} x_{j}\right)$

[57] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Łukasz Kaiser, and Illia Polosukhin. 2017. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS). 1–11.

在第二个算法中 GNN Model Training 提出了几个要求：

权重随机初始化、多 epoch、训练多个 GNN，选取最佳 loss (-> 0) 最少 cost 的模型

[!note] 输入层 
如前文所述，GNN 模型的输入是一个单位星图 $g_{v_i}$ （或者其星子结构 / 子图，记为 $s_{v_{i}}$ ）。 $g_{v_i}$ （或者 $s_{v_{i}}$ ）中的每个顶点 $v_{j}$ 都关联一个大小为 $F$ 的初始特征向量 $x_{j}$ ，而该向量是通过 顶点标签编码或者独热编码 [12] 获得的。
GAT 模型中所提及的

Readout

读出层 [65, 68] 为整个单位星图生成一个嵌入向量，它是通过对 $g_{v_{i}}$ 中所有顶点 $v_{j}$ 的特征向量求和得到的，并且这个操作是置换不变的。也就是说，我们得到

$y_{i}=\sum_{\forall v_{j} \in V\left(g_{v_{i}}\right)} x_{j}'$

Fully Connected Layer：得到中心顶点 $v_{i}$ 的嵌入向量 $o(g_{v_{i}})=\sigma(\mathbb{W}y_{i})$

# Node Dominance Embedding

GNN Model Training. To guarantee that we do not lose any candidate vertices for exact subgraph matching, we train (or even overfit the GNN model until the loss function $L(\cdot)$ (given in Eq.(7) is equal to 0. Intuitively, from Eq. (7), when the loss function $L(D_{j})$ $=0$ holds, the embedding vector $o(s_{v_{i}})$ f any star substructure $s_{v_i}$ is dominating [14] (or equal to) that, $o(g_{v_{i}})$ , of its corresponding unit star graph $g_{v_{i}}$ .In the sequel, we will simply say that $o(s_{v_{i}})$ dominates $o(g_{v_{i}})$ denoted as $o(s_{v_{i}}) ≤o(g_{v_{i}}))$ if $o(s_{v_{i}})[t] ≤o(g_{v_{i}})[t]$ for all $1 ≤t ≤d$ (including the case where $o(s_{v_{i}})=o(g_{v_{i}}))$

# 基于 GNN - PE 的子图匹配算法

剪枝策略
- 路径标签剪枝：通过比较路径上孤立顶点的嵌入向量构建的路径标签嵌入向量来判断是否剪枝。
- 路径支配剪枝：根据路径嵌入向量的支配关系判断是否剪枝。
索引机制
- 在子图分区中提取长度为 (l) 的路径，计算其路径支配嵌入向量并构建聚合 R * - 树索引，索引节点中存储路径嵌入向量的相关信息用于剪枝。
索引级剪枝
- 包括索引级路径标签剪枝和索引级路径支配剪枝，根据索引节点中的信息判断是否剪枝路径。
匹配算法
- 给定查询图，先获取查询路径，生成相应的嵌入向量，然后遍历索引获取候选路径集，最后精炼候选路径并连接匹配路径得到匹配子图。

# 4. 成本模型和查询计划

成本模型
- 定义查询成本 (Cost_{Q}(\varphi)=\sum_{p_{q}\in Q} w (p_{q}))，其中 (w (p_{q})) 可通过顶点度数或在支配区域中的候选路径数量等方式计算。
查询计划选择
- 根据成本模型选择查询计划，包括选择起始顶点，获取初始路径，逐步扩展路径集并选择成本最小的路径集作为查询路径。

# 5. 实验验证

实验设置
- 在 Ubuntu 服务器上进行实验，使用 PyTorch 实现 GNN 训练，(C++) 实现在线子图匹配，对比了 8 种代表性子图匹配基线方法，使用真实和合成图数据集，设置了不同的参数进行实验。
实验结果
- 参数调整：分析了路径长度、GNN 数量、查询计划选择策略等参数对 GNN - PE 性能的影响。
- 有效性评估：验证了提出的剪枝策略在真实和合成图上的有效性，剪枝率可达 99.17% - 99.99%。
- 效率评估
  - 在真实和合成图数据集上，GNN - PE 方法的效率优于基线方法，对于大规模图能取得更好的性能。
  - 分析了不同参数（如数据图平均度、查询图模式、图大小等）对 GNN - PE 效率的影响，验证了其在不同情况下的高效性和可扩展性。
  - 评估了离线预计算成本，包括图分区、GNN 训练和索引构建时间。

子图匹配

NP-C 复杂度降为多项式复杂度

GNN 精确图匹配

将模式切为路径覆盖的模式

partition 分割

和 querymatch

论文