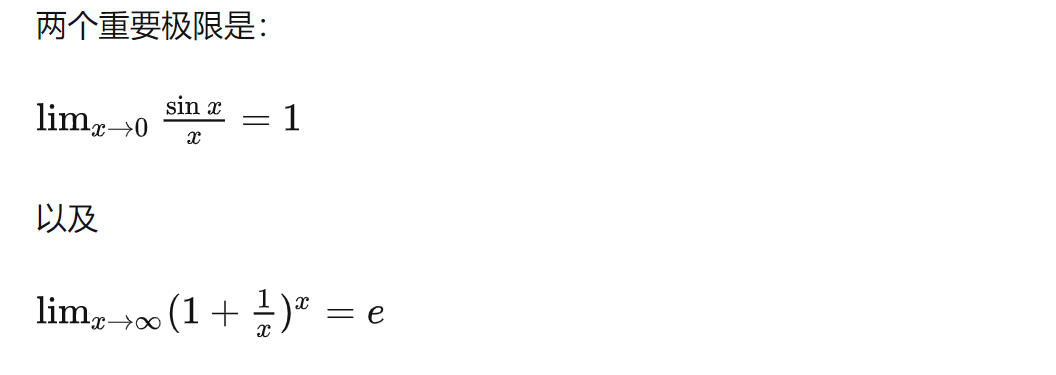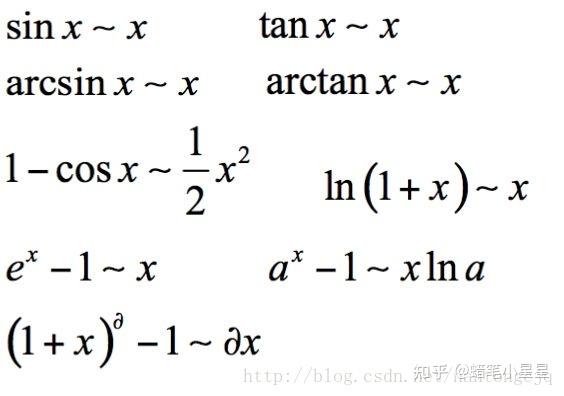# 数学笔记・二

# 第四节 函数的连续性（承第一章函数与极限）

• 连续性概念

  由极限的性质可知，一个函数在某点连续的充要条件是它在该点左右都连续。

• 间断点分类

  • 第一类间断点

    可去间断点：函数在该点左极限、右极限存在且相等，但不等于该点函数值或函数在该点无定义。如函数 y=（x^2-1)/(x-1) 在点 x=1 处。

    跳跃间断点：函数在该点左极限、右极限存在，但不相等。如函数 y=|x|/x 在点 x=0 处。

  • 第二类间断点

    无穷间断点：函数在该点可以无定义，且左极限、右极限至少有一个不存在，且函数在该点极限为∞。如函数 y=tanx 在点 x=π/2 处。

    振荡间断点：函数在该点可以无定义，当自变量趋于该点时，函数值在两个常数间变动无限多次。如函数 y=sin (1/x) 在 x=0 处。

  • 由上述对各种间断点的描述可知，函数 f (x) 在第一类间断点的左右极限都存在，而函数 f (x) 在第二类间断点的左右极限至少有一个不存在，这也是第一类间断点和第二类间断点的本质上的区别。

# 第五节

• 迫敛准则

  主要是放缩，抓住可合成量（如 N 个 1 求和为 n*(n+1)/2），和高阶量不变原则

• 单调有界准则

  单调有界数列必有极限。用于证明收敛很有用。

  求极限时可以先假设存在。方便计算。（避免求数列通项）

• 两个重要极限

  第二个很重要，第一个可以直接看成等价无穷小。

# 第六节

• 无穷小量

  确切地说，当自变量 x 无限接近 x₀（或 x 的绝对值无限增大）时，函数值 f (x) 与 0 无限接近，即 f (x)→0 (或 f (x)=0)，则称 f (x) 为当 x→x₀(或 x→∞) 时的无穷小量。

• 等阶无穷小量

  即两个无穷小量坐商得常数时。

• 等价无穷小量

  即两个无穷小量坐商得 1。等价无穷小量可互换。

• 常见等价无穷小量

关于我突然变水的原因：

实在是比较忙，各项内容也越来越复杂，所以就择取主要的知识点并舍去证明。

以上。

# 第二章

# 导数

• 导数定义

  函数可导一定连续，函数连续不一定可导。

• 求导法则

  注意除法，反函数，隐函数求导法则。

  掌握反代的思想，掌握对数求导法。

• 含参求导

  一阶导可直接求二阶导可能需要反代。

注意导数与微分的关系，如何二阶导隐函数。以及推导方法。

• 断点处的导数求解，在有定义时使用求导法。

  在无定义时，使用定义法。(求极限)

• 高阶函数求导注意规律，和复合函数的导

# 微分

• 一元函数，可导则可微

• 微分常数 A，与极限有关

• 微分运算类似求导法则

• 微分近似运算

  f(x)=f(x0)+f'(x0)(x-x0)

  为了计算 f (x)，可找一个邻近于 x 的 x0，只要 f (x) 和 f'(x) 容易计算，就可以利用这个公式计算 f (x) 的近似值。

# 第三章

# 微分中值定理

• 费马引理

• 罗尔中值定理

• 拉格朗日中值定理

• 柯西中值定理

洛必达法则

泰勒公式

麦克劳林公式

• 佩亚诺余项

  高阶无穷小

• 拉格朗日余项

  中值 -- 定量分析

函数的凹凸性

# 第四章

# 不定积分

# 换元积分

# 分部积分

凑微分，低次换元，三角换元，二次换元，重复型

# 积分表

# 有理函数的不定积分

待定系数法

• 万能公式

# 定积分

# 定积分概念求无穷项和的极限

# 估值定理

区间内的 Max 与 Min 乘以区间长度得到限定区间。

# 积分中值定理

求积分函数极限时用到，由介值定理推得

# 几何意义

# 牛顿莱布尼茨公式

# 微积分学基本定理

连续函数必存在原函数

# 平面曲线的弧长与曲率

# 极坐标系

x=pcosa,y=psina;

# 平面曲线的曲率

# 曲率圆

# 定积分的几何应用

# 连续函数的平均值

# 定积分在物理学与经济学

• 变力做功

• 引力问题

• 液体侧面压力

# 反常积分