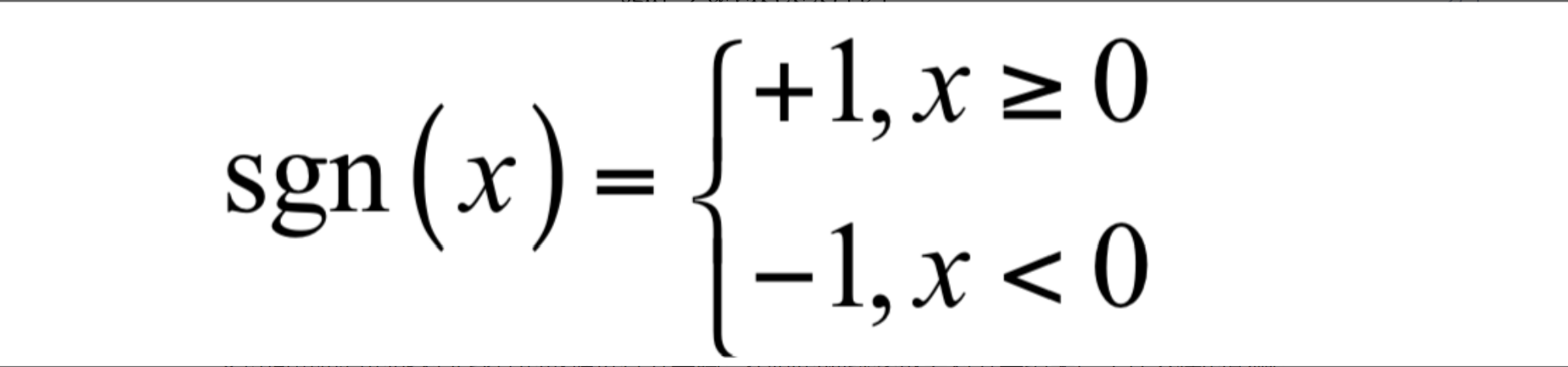# 高等数学・一
学习时做的一些笔记,顺便对内容梳理一遍。^0
# 第一章 函数与极限
# 第一节 映射与函数
映射
与 x 所对应的 y 称为 x 在映射 f 下的象。
x 称为 y 在 f 下的原象。满射、一一映射、单射、双射
A 映射得到的 B 集合等于映射的目标集合则是满射。
对每个 y 都有唯一一个 x 对应,则是单射或称一一映射。
若 f 既是满射又是单射则称为双射。
函数定义与表示方法
特殊函数
狄利克雷函数
![狄利克雷函数 00_2]()
狄利克雷函数是一个定义在实数范围上、值域不连续的函数。狄利克雷函数的图像以 Y 轴为对称轴,是一个偶函数,它处处不连续,处处极限不存在,不可黎曼积分。这是一个处处不连续的可测函数。
符号函数
![符号函数 00_3]()
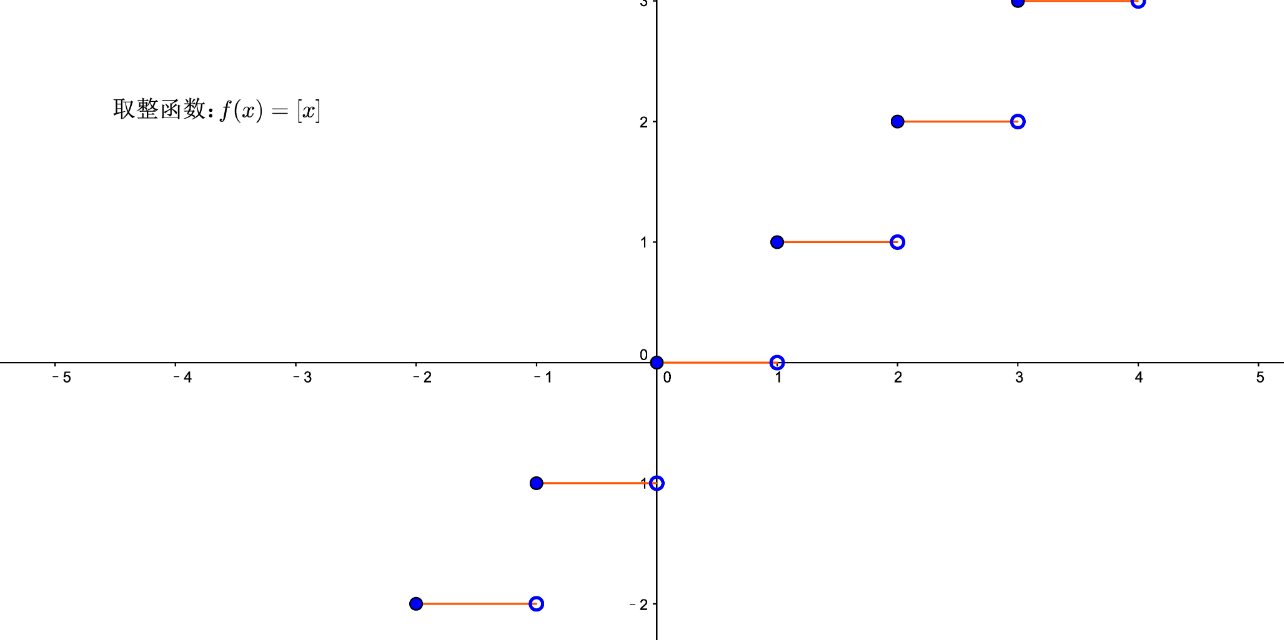
取整函数
![image-20220914131129520]()
函数 y=[x] 称为取整函数,也称高斯函数。其中不超过实数 x 的最大整数称为 x 的整数部分,记作 [x]。该函数被广泛应用于数论,函数绘图和计算机领域。
函数的有界性
函数 f (x) 在 D 上有界的充要条件是 f (x) 在 D 上既有上界又有下界。
函数的单调性
- 单调增 (减) 函数
- 严格单调增 (减) 函数
函数的四则运算
复合函数
形如: f(g(u(x))) 或 f o g o u
反函数
反函数的单调性基本归纳于 先外后内,同增异减。
初等函数
初等函数是由幂函数(power function)、指数函数(exponential function)、对数函数(logarithmic function)、三角函数(trigonometric function)、反三角函数(inverse trigonometric function 与常数经过有限次的有理运算(加、减、乘、除、有理数次乘方、有理数次开方)及有限次函数复合所产生,并且能用一个解析式表示的函数。
# 第二节 数列的极限
邻域
- 邻域
- 去心邻域
- 左 (右) 邻域
数列基本概念
有限 or 无限
通项公式
整标函数
子数列
单调性
作差或作商求单调性。有时候利用数列的单调性可能会得到惊喜的解题方式。
数列极限
收敛数列与数列的有界性
tip:数列收敛一定有界,数列有界不一定收敛
- 极限唯一性 & 有界性 & 保号性
极限四则运算法则(严格意义上要分别证明数列的与函数的)
# 第三节 函数的极限
函数极限
![00_1]()
函数某点极限存在的充要条件是左右极限都存在且相等。
海涅 (Heine) 定理
求函数极限
- 简单的有限次函数,如果最高次项系数相等比较最高次项系数,如果不等,次数高的为高阶无穷大量。
- 妙用,分子有理化,分母有理化。
- 通分消去。
- 立方差、因式分解。
- 裂项等将无穷项收缩的方法。
- ......
复合函数极限
# 第四节 函数的连续性
连续性概念
由极限的性质可知,一个函数在某点连续的充要条件是它在该点左右都连续。
间断点分类